A Parte 2 de nossa série sobre tudo que envolve privacidade na Web3 explora a computação segura e esclarece equívocos sobre tudo, desde ZKPs até TEEs!

Bem-vindo de volta ao Beyond ZK (Além do ZK) — uma série de blogs da comunidade Secret Network explorando soluções pragmáticas para privacidade Web3.

Na primeira parte deste blog , demos uma primeira olhada no problema de computação segura em Web3. Blockchains são uma ferramenta incrível para assertividade— mas eles têm compensações e complicações importantes em relação à privacidade. Como as blockchains não são soluções que priorizam a privacidade, a Web3 pode ser pior em termos de privacidade do que o Web2 já foi. A falta de computação privada na blockchain significa que todos podem ver todos os seus dados, forçando os desenvolvedores a construir em um espaço de design estreito que não lhes permite criar aplicativos descentralizados verdadeiramente úteis.

Na Parte 2 desta série de blogs, vamos nos aprofundar na caixa de ferramentas de criptografia e procurar possíveis soluções pragmáticas para o problema de privacidade introduzido por blockchains. O conjunto diversificado de métodos que examinaremos hoje são:

• Criptografia Parcial ou Totalmente Homomórfica (HE/FHE)
• Computação multipartidária segura (MPC)
• Ambientes de Execução Confiáveis ​​(TEEs)
• Provas de conhecimento zero (ZKPs)

Na criptografia, raramente há um método “ideal”. Cada solução mencionada aqui tem múltiplas construções e pode ser usada sozinha ou em conjunto com outras soluções para resolver problemas interessantes caso a caso. Cada construção e combinação vem com trade-offs e vantagens relativas.

Neste post, estamos interessados ​​em como os métodos mencionados acima podem ser usados ​​individualmente para resolver o problema generalizado de privacidade: como executar qualquer computação em uma configuração de blockchain com exatidão, garantindo que os nós/validadores/mineradores subjacentes não possam ver os dados que eles estão computando.

Esse estado de computação privada generalizada será referido como computação segura no restante deste blog. À medida que avançamos neste exercício, também abordaremos algumas soluções para problemas específicos de privacidade no espaço blockchain (por exemplo, envio de tokens de forma privada).

Vamos! 🚀

Fully Homomorphic Encryption (FHE)

A criptografia totalmente homomórfica (FHE) é uma ideia fácil de entender, mas extremamente difícil de implementar. Na verdade, embora a ideia original tenha sido proposta em 1978 por Rivest et al, não foi até 2009 que Craig Gentry construiu a primeira construção de tal esquema. Este avanço inaugurou uma década de interesse renovado e pesquisa em esquemas de criptografia totalmente homomórficos, que melhoraram muito a eficiência da construção original em muitas ordens de magnitude.

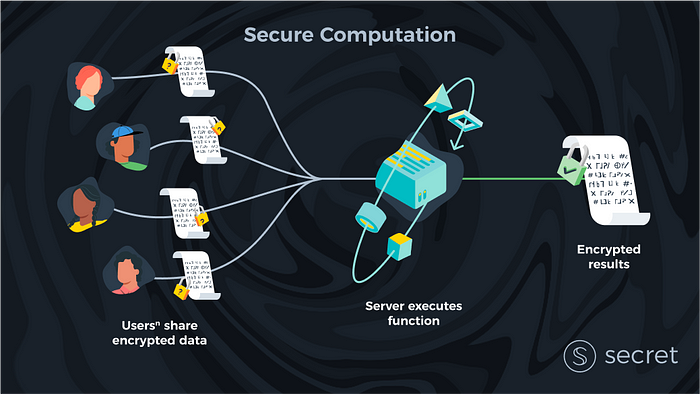
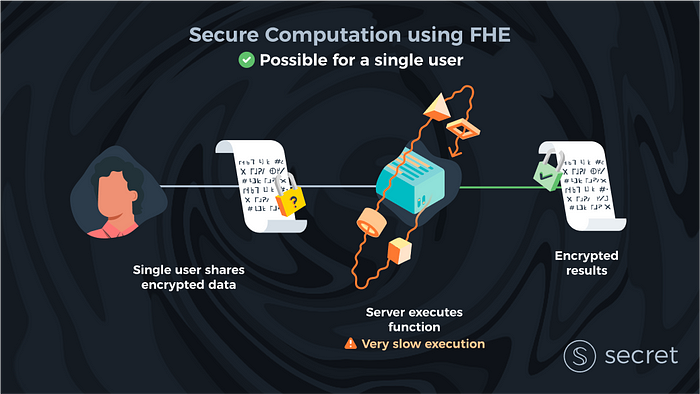
Então, o que exatamente é FHE? FHE é um esquema de criptografia que permite a qualquer pessoa calcular dados criptografados sem precisar descriptografá-los primeiro. Relembrando nosso primeiro post desta série, vamos imaginar novamente uma versão simplificada do mundo ideal em que existe um único cliente/usuário (em vez de muitos) e um servidor. O problema neste mundo ideal é que não podemos confiar naquele servidor para proteger a privacidade de nossos dados. Bem, com o FHE, isso parece trivial: um cliente pode enviar seus dados para um servidor criptografado, e o servidor pode calcular seus dados sem visualizar os dados brutos. Tarefa concluída?

Limitações da FHE

Primeiro, o FHE, até o momento, tem sido extremamente ineficiente. O FHE é, de fato, a mais lenta de todas as tecnologias de preservação da privacidade que conhecemos. No entanto, a eficiência da computação FHE vem melhorando a uma taxa incrível, e o hardware especializado (CPU → GPU → FPGA → ASICs) melhorará ainda mais a velocidade da computação em várias ordens de magnitude na próxima década. Esse aumento de eficiência é o motivo mais importante pelo qual a comunidade Secret está analisando o FHE novamente como uma solução potencialmente viável ( conforme mencionado na postagem do fórum Secret 2.0) .

No entanto, é importante esclarecer que, mesmo em 5 a 10 anos, é mais provável que o uso dos recursos de FHE só faça sentido para determinados casos de uso ou para determinadas partes da execução de contratos inteligentes. Por exemplo, você pode querer usar o FHE para armazenar e operar dados extremamente confidenciais (e pequenos), como chaves criptográficas ou SSNs.

FHE com vários clientes

Portanto, o FHE é uma solução aparentemente simples, embora computacionalmente cara, quando o problema de computação envolve apenas um cliente. Então a questão se torna: como introduzimos um segundo cliente nesse problema de computação segura? Deve ficar evidente que, na prática, a configuração de computação segura com vários clientes é a configuração mais interessante, pois muitos cenários envolvem a combinação de dados de várias partes.

Em um mundo com apenas um cliente, ela mesma poderia alugar um servidor de nuvem forte e executar cálculos em vez de confiar seus dados a terceiros. Nesse caso de cliente único, o problema de confiar em uma parte externa para manter seus dados privados e executar cálculos para você corretamente parece menos importante na prática.

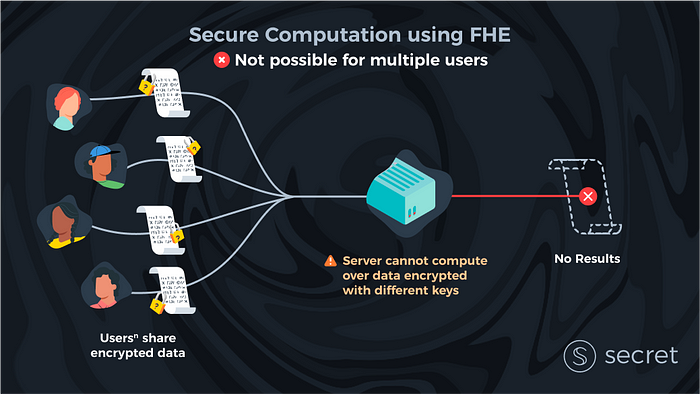
Adicionar esse segundo cliente não é uma mudança trivial e deixa muitos técnicos coçando a cabeça. Primeiro, vamos imaginar que existam apenas dois clientes no mundo. Ambos os clientes têm suas próprias entradas e desejam calcular uma função sobre suas entradas. Como de costume, ambos querem privacidade (ou seja, nem o servidor nem o outro cliente ficam sabendo de seus dados). Com FHE ‘puro’, não está claro como fazer isso, pois cada cliente usou sua própria chave para criptografar seus dados. O FHE é incrível, mas não pode calcular magicamente dados criptografados com chaves diferentes. Então, como resolvemos isso?

Partial Homomorphic Encryption (PHE)

A resposta honesta é que muitos métodos são necessários para resolver esse problema. Além da criptografia totalmente homomórfica, que pode calcular qualquer função arbitrária sobre dados criptografados, existem muitos esquemas de criptografia parcialmente homomórfica (HE ou PHE). Esses esquemas parciais podem calcular funcionalidades específicas — geralmente adição ou multiplicação — mas não ambas (observe que todas as funções podem ser reduzidas a operações de adição e multiplicação). Esses esquemas HE parciais foram inventados décadas atrás e são muito mais eficientes, e podem ser suficientes para um conjunto limitado de casos de uso, mas não são suficientes para o caso geral de computação segura.

Várias redes visam usar um esquema parcial como o PHE para obter privacidade (por exemplo, Penumbra e Dero). No entanto, é importante entender que eles não podem, por definição, oferecer suporte a contratos inteligentes de uso geral. As aplicações dessas técnicas para blockchains com foco na privacidade são novas, mas os casos de uso que podem suportar são bastante limitados.

Existem maneiras não triviais de estender a variedade de aplicativos aos quais você pode dar suporte com uma solução parcial como essa, mas isso exigiria profundo conhecimento em criptografia. Esses aplicativos geralmente trazem outras compensações ocultas que são difíceis de entender. Por esse motivo, o PHE provavelmente nunca permitirá que os desenvolvedores criem aplicativos arbitrários com privacidade.

Portanto, se as soluções FHE ou HE parcial sozinhas não puderem resolver o problema de computação segura de vários clientes… o que pode?

Secure Multi-party Computation (MPC)

Computação multipartidária (MPC) refere-se tanto ao problema — fazer cálculos arbitrários sobre dados criptografados fornecidos por várias partes — quanto a um dos métodos destinados a resolvê-lo.

Para evitar confusão, tomamos cuidado ao longo deste post para nos referirmos ao problema como ‘computação segura’ e reservamos o uso de MPC para nos referirmos a uma gama específica de soluções que resolvem diretamente este problema.

Geralmente, existem dois tipos de soluções de MPC: as baseadas em Compartilhamento Linear de Segredos e as baseadas em Circuitos Garbled . Descrever essas soluções está fora do escopo desta postagem, mas as compensações e o modelo de segurança em que operam são importantes para nossa compreensão.

MPC com vários clientes

As soluções MPC podem ser vistas como a solução de sistemas distribuídos (ou, se preferir, o “blockchain-ish”) para computação sobre dados privados. Nesses esquemas, em vez de confiar em um único servidor, temos vários servidores não confiáveis ​​que, em conjunto, executam uma computação sobre os dados do cliente. Alterar as suposições de confiança aumenta muito o espaço de solução. As soluções de MPC são desenvolvidas com vários clientes em mente, o que significa que não há problemas teóricos com servidores combinando dados de qualquer número de clientes, como em uma configuração de FHE.

Observe que a maneira de transformar um esquema FHE para um usuário em um para vários usuários é realmente “MPC” dividindo uma única chave de criptografia FHE em compartilhamentos compartilhados por todos os servidores. Isso é chamado Threshold FHE , que mistura MPC com FHE. Do ponto de vista da segurança, reduz-se ao mesmo modelo de segurança do MPC. O TL;DR disso é que usar o FHE para vários usuários é essencialmente outra forma de MPC. Exploraremos isso com mais profundidade em um post futuro.

Limitações do MPC

Obviamente, também há compensações no uso do MPC. A principal desvantagem é que o MPC depende da “segurança por não conluio”. O uso do FHE permite que o cliente mantenha sua chave de criptografia secreta sem que o servidor tenha acesso aos seus dados. Mas com o MPC, precisamos de pelo menos um servidor para ser honesto, porque se todos os servidores entrarem em conluio, eles podem reconstruir trivialmente os dados privados. Na verdade, isso ocorre por design porque as soluções MPC não contêm chaves.

Em vez disso, o MPC oculta os dados dando a cada servidor um compartilhamento “criptografado” dos dados, de forma que você precise de todos os compartilhamentos para “”descriptografar” os dados. Além disso, cada compartilhamento sozinho não revela nada sobre os dados de texto simples. A partir disso, deve ficar claro que o requisito de conluio é inerente e pelo menos uma das partes precisa agir honestamente.

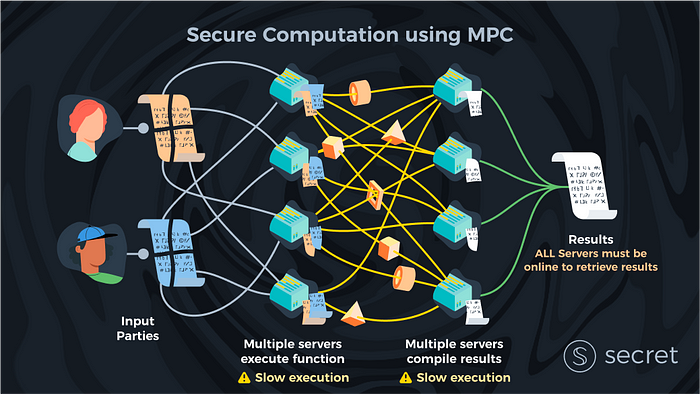
Na prática, pode-se adaptar os limites de conluio para otimizar a vivacidade ou a privacidade. No exemplo acima, onde todos os compartilhamentos de chaves são necessários para reconstruir os dados, obtemos o máximo de privacidade. No entanto, é necessário apenas um único servidor para montar um ataque DoS contra todo o sistema. Isso ocorre porque leva apenas um servidor que não responde à solicitação de um cliente e o resultado não pode ser computado. Podemos, no entanto, optar por exigir apenas ½ (ou qualquer quantidade arbitrária) dos compartilhamentos de chave, o que significa que exigimos que a maioria dos servidores seja honesta e não seja conivente para poder fornecer um resultado computacional.

Há muito mais a dizer sobre esse tópico, mas, por enquanto, é importante notar a semelhança entre blockchains e soluções de MPC. Ambos são sistemas distribuídos que baseiam sua segurança em suposições anti-conluio, o que significa que há uma compensação inerente entre correção, vivacidade e privacidade. Agora fica a pergunta: o que é mais importante?

MPC para privacidade versus correção

Agora que consideramos a compensação entre correção e vivacidade, vamos abordar de frente por que a privacidade é provavelmente mais difícil do que a correção nos sistemas MPC. A correção é verificável — se uma transação for adulterada, isso é visto ou o consenso é interrompido. No entanto, não se pode verificar ataques de conluio à privacidade, tornando-o um ataque ‘silencioso’. Se os servidores do sistema compartilharem seus compartilhamentos de chaves fora dos limites do sistema, eles podem entrar em conluio e nunca saberemos que eles reconstruíram os dados. Esse vetor de ataque silencioso torna a solução de privacidade com sistemas distribuídos mais desafiadora do que garantir a correção.

Para eliminar esse vetor de ataque, podemos ter o maior número possível de servidores executando os cálculos, evitando assim ataques de conluio. Infelizmente, o MPC escala mal com o número de partes e aumentar o número de servidores prejudica a vivacidade. Portanto, parece que o MPC sozinho não é suficiente e outras tecnologias que dificultam o conluio precisam ser implementadas.

Conluio complicador

Uma maneira de dificultar o conluio do MPC seria forçar todos os servidores no sistema distribuído a usar Ambientes de Execução Confiáveis ​​(mais sobre isso abaixo). Nosso objetivo é implementar uma solução de cross-método na atual rede principal da Secret, trazendo segurança adicional ao nosso sistema de privacidade.

Como alternativa, pode-se complicar o conluio trabalhando em uma configuração permitida, onde os servidores são (parcialmente) confiáveis ​​e podem ser reidentificados se ocorrer um vazamento de dados. Esta é a direção que a Partisia Blockchain parece estar tomando: um conjunto off-chain de nós semiconfiáveis ​​executa cálculos privados, e a blockchain apenas armazena e verifica o estado.

Outros métodos incluem o design mencionado em minha tese de pós-graduação e o white paper original da Enigma. Nesses artigos, um mecanismo é proposto para amostragem de pequenos comitês para executar cálculos. Se feito com cuidado, podemos projetar uma blockchain que tenha muitos servidores diferentes, mas para cada computação (ou conjunto de computações) selecione um pequeno número de partes para realmente fazer o trabalho pesado. Embora essa solução pareça promissora e tenha uma escala muito boa, ela não é prática por muitos motivos que, na maioria das vezes, voltam a ter que confiar em uma ou várias partes.

Iremos nos aprofundar nesses tipos de combinações de técnicas na Parte 3 desta série de blogs, portanto, fique atento!

Trusted Execution Environments (TEEs)

Até agora, todas as soluções para o problema de computação segura que mencionamos foram de natureza criptográfica. “Criptográfico” geralmente significa “legal” aos olhos dos desenvolvedores, mas “legal” nem sempre significa eficiente, pragmático ou mesmo viável. Até agora, o único método puramente criptográfico que poderia resolver o problema de computação segura é o MPC, que ainda assume que os servidores (por exemplo, nossos validadores de blockchain) não conspiram ou não podem conspirar para reconstruir os dados. Então, vamos dar uma olhada em outra solução potencial para o problema em questão.

Um Ambiente de Execução Confiável (TEE), em termos simples, é uma região no processador separada do restante da CPU. Essa região pode armazenar dados (por exemplo, chaves de criptografia) e executar cálculos que não podem ser adulterados pelo host da máquina. Além disso, o host não pode extrair nenhum dado armazenado nessa região (pelo menos, em teoria).

Como os TEEs resolvem a privacidade (e correção)

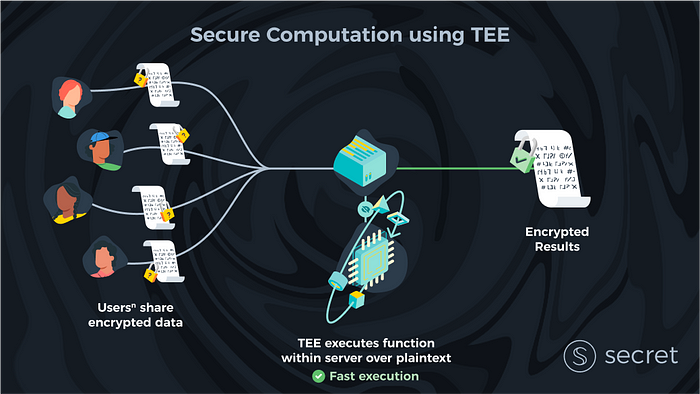
Os TEEs podem resolver a privacidade e correção exigindo que nosso servidor (ou na configuração de blockchain, servidores) execute todos os cálculos dentro de seu TEE. Além disso, podemos solicitar aos clientes que criptografem seus dados de entrada usando uma chave que também está disponível apenas nos TEEs dos servidores.

Com esse design, ninguém — nem mesmo o host que possui os servidores — tem acesso aos dados dos clientes. Isso ocorre porque os dados só são descriptografados e calculados dentro do TEE. Para obter mais informações sobre como esse sistema funciona na prática e como as chaves de criptografia são mantidas em segurança, consulte a documentação técnica da Rede Secret .

Outra maneira de pensar nos TEEs é como uma aproximação de hardware do mundo ideal que descrevemos na Parte 1 , onde há um único servidor confiável que pode executar cálculos de forma correta e privada. No entanto, tirar o máximo proveito dos TEEs é muito mais complicado do que descrevemos aqui. Para evitar ataques de censura ou DoS, ainda é melhor usar TEEs em um sistema distribuído como blockchain em vez de depender de um único servidor.

Como os sistemas TEE obtêm segurança por meio da dependência de hardware em oposição à criptografia pura, eles são muito eficientes. Embora as soluções criptográficas sejam geralmente ordens de magnitude mais lentas do que a computação em claro, na maioria dos casos os TEEs têm menos de 40% de sobrecarga no tempo de computação. Isso vem principalmente do requisito de descriptografar a entrada e criptografar novamente a saída para preservar a privacidade.

Desvantagens dos TEEs

A principal desvantagem dos TEEs que preocupa os usuários é a possibilidade de ataques de canal lateral. Nos últimos anos, os pesquisadores mostraram como podem extrair informações dos TEEs usando principalmente a execução especulativa, um método usado por todos os processadores modernos para ganhar eficiência. Embora a maioria desses problemas possa ser resolvida em software ou hardware e seja difícil de explorar na prática, eles apresentam uma desvantagem em comparação com técnicas criptográficas puras nesse vetor de ataque específico. Bugs de arquitetura (que podem afetar qualquer tipo de hardware, não apenas enclaves seguros) também são possíveis e representam um risco sério, que não deve ser ignorado.

Com essas compensações consideradas, os TEEs ainda são a melhor solução prática, especialmente para cálculos de alto desempenho em dados de baixa sensibilidade. Mesmo quando o núcleo de uma solução em potencial é de natureza criptográfica, os TEEs são essenciais para aumentar a segurança e podem ajudar a evitar conluio enquanto aumentam a escalabilidade. É por isso que a Secret continua a construir com a tecnologia TEE e a implementá-la em nossas soluções.

Zero-Knowledge Proofs (ZKPs)

Por último, mas não menos importante, queremos abordar o uso de Provas de Conhecimento Zero (ZKPs) para o problema de privacidade Web3. Como uma rede, muitas vezes recebemos perguntas sobre como o projeto X se compara à Secret, onde X é um projeto que utiliza alguma técnica baseada em Provas de Conhecimento Zero. Se for esse o caso, por que deixamos os ZKPs para o final deste longo post?

Bem, como se vê, os ZKPs não são realmente uma solução de privacidade — pelo menos não para o grande problema de privacidade que descrevemos nesta série de postagens. Mas antes de podermos explicar o porquê, precisamos explicar brevemente o que são ZKPs.

Um sistema de prova de conhecimento zero é um protocolo bipartido no qual um provador P deseja provar a algum verificador V que alguma afirmação é verdadeira, sem revelar mais nada. Sem ficar muito formal, o provador geralmente fornece uma prova que diz ‘Eu calculei y=f(x) corretamente’, onde o verificador conhece a função f e a saída y , mas não os dados de entrada x .

Por exemplo, imagine que Alice tenha um passaporte digital certificado e queira provar ao barman que ela é maior de 21 anos sem revelar sua data de nascimento. Nesse caso, f é o cálculo ‘Tenho mais de 21 anos?’, x é o passaporte certificado que inclui a data de nascimento e y é a resposta (Verdadeiro ou Falso). Usando ZKPs, Alice pode conseguir isso.

Os ZKPs existem há várias décadas. Na última década, uma forma especial de ZKPs foi introduzida — uma que torna a prova em si extremamente pequena (existem várias variantes disso com diferentes compensações) e a verificação extremamente rápida e eficiente. Essas provas também não são interativas. Isso significa que um provador pode gerar uma prova de uma só vez, enviá-la ao verificador e o verificador pode executar a verificação de forma independente sem entrar em contato com o provador novamente. Gerar a prova em si é caro, dependendo da complexidade do cálculo, mas isso também teve grandes melhorias nos últimos anos.

Por que os ZKPs funcionam melhor para dimensionamento do que para privacidade

Essas propriedades de computação não interativas e leves do lado do verificador tornam os ZKPs uma ótima maneira de escalar blockchains fora da rede.

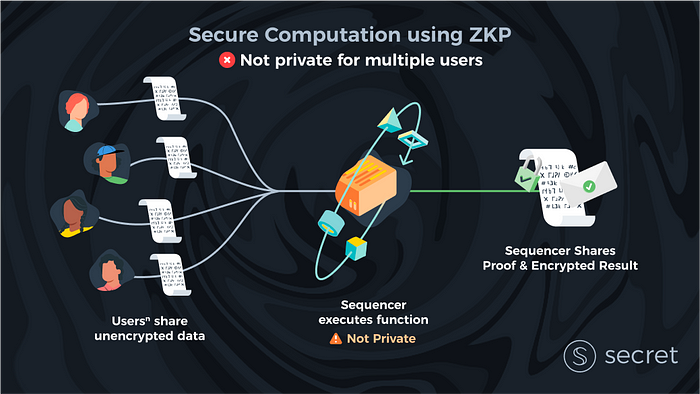
A ideia principal é bastante simples: fazer com que uma parte centralizada (geralmente chamada de sequenciador) execute todas as transações (e cálculos) fora da cadeia. Isso significa que os clientes interagem diretamente com esse sequenciador em vez da blockchain e enviam seus dados de entrada não criptografados. O sequenciador, após executar todos os cálculos, produz uma prova sucinta e a envia para a blockchain junto com as saídas (geralmente o estado atualizado). A blockchain, que atua como o verificador, verifica se a prova está correta e, se estiver, aplica as mudanças de estado sem aprender os dados dos clientes diretamente. Todas as soluções blockchain ZK de uso geral usam esse método de escalonamento, incluindo zkEVMs (dos quais existem alguns), Aleo, Starkware e outros.

Mas, embora os ZKPs sejam uma ótima ferramenta de dimensionamento, deve ficar claro por que os ZKPs oferecem uma solução de privacidade limitada para Web3. Os usuários precisam confiar em um sequenciador centralizado (assim como na Web2) com todos os seus dados. Da mesma forma, se quisermos permitir vários sequenciadores (para distribuir a suposição de confiança), a situação de privacidade só piora.

O uso restrito de ZKPs para privacidade

No entanto, em certas situações, pode-se usar ZKPs para fornecer privacidade. Um exemplo disso é a Zcash, onde cada usuário tem que provar que não está gastando moedas duplamente. Eles têm que provar isso sem revelar a blockchain quantas moedas eles têm ou estão transferindo para quem. De um modo geral, a chave para usar ZKPs dessa maneira é que cada usuário faz uma computação em sua própria parte de um estado privado compartilhado globalmente. Eles então usam um ZKP para provar a blockchain que não trapacearam.

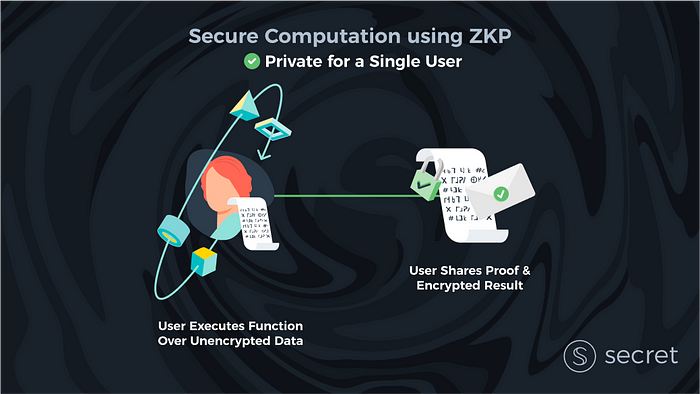
Mas precisamos ser claros: essa técnica é limitada a casos de uso muito específicos, não a computação segura generalizável. Por exemplo, um leilão que compara lances privados de clientes não pode usar essa técnica, porque precisa usar diretamente as entradas de vários clientes como parte do cálculo. Os clientes teriam que compartilhar dados fora da rede para fazer provas como essa e, assim, renunciar à privacidade de seus dados. Além disso, definir contratos inteligentes de uma forma que facilite isso requer profundo conhecimento criptográfico e muitas vezes tem outras compensações em termos de implantação (por exemplo, forçar os clientes a fazer criptografia pesada localmente).

A conclusão disso é que os ZKPs são mais uma solução de dimensionamento do que uma solução de privacidade. Os ZKPs podem solucionar a privacidade em alguns casos de uso limitados a clientes únicos, como privacidade transacional. Cálculos mais complexos requerem adaptação significativa de circuitos e podem nunca ser viáveis, a menos que confiemos totalmente nos sequenciadores para proteger as informações do usuário. Os ZKPs, portanto, não podem resolver o problema de computação segura por conta própria. No entanto, eles podem ser uma boa ferramenta adicional para dimensionar camadas de base privadas mais lentas ou como uma ferramenta complementar para MPC e FHE. Combinar técnicas dessa maneira é algo que abordaremos em um post futuro.

Resumo

Neste ponto, examinamos praticamente toda a caixa de ferramentas de privacidade (exceto privacidade diferencial e algumas outras soluções não relacionadas). Embora cada solução apresentada aqui tenha décadas de pesquisa e muitos milhares de documentos por trás dela, as compensações inerentes permanecem as mesmas e podemos resumi-las aqui.

Como um lembrete: o problema geral em que estamos interessados ​​é o da computação segura , que questiona como vários clientes podem executar cálculos sobre seus dados compartilhados enquanto garantem a correção e a privacidade . Explicamos que blockchains resolvem apenas a primeira metade do problema (correção) e apresentamos várias tecnologias possíveis que resolvem o segundo problema (privacidade).

Resumimos as soluções disponíveis e suas compensações na tabela abaixo. Observe que esta é uma simplificação exagerada dessas ferramentas e das suposições que elas fazem — nosso objetivo é apresentar apenas as maiores compensações e preocupações de segurança ao escolher uma (ou mais) dessas ferramentas. Por esse motivo, ignoramos suposições criptográficas subjacentes, segurança quântica ou suposições de configuração confiáveis ​​que podem ou não existir com base em uma construção específica.

A tabela acima “comprime” ao máximo as dimensões de interesse no que diz respeito a suposições de segurança, eficiência (divisão entre computação local e custos de rede) e como é fácil para os desenvolvedores usar essa ferramenta na prática.

A partir disso, a pergunta mais importante que se deve fazer é: qual é a melhor suposição a ser feita na prática? Que os validadores nunca conspirarão para vazar os dados (soluções Threshold FHE/MPC)? Ou é melhor confiar em uma parte centralizada para armazenar e ver todos os dados (soluções ZKP)? Ou é melhor confiar que ataques de canal lateral (ou bugs de hardware que expõem vulnerabilidades) contra TEEs podem ser protegidos com eficiência?

Pode ser que não haja uma resposta clara para essa pergunta, mas pelo menos deve fazer você pensar. Neste momento, parece que os TEEs ainda apresentam a única solução prática para casos de uso de baixa a média sensibilidade e alto desempenho. Para qualquer coisa além, parece que a combinação de MPC/Threshold FHE com TEEs é o caminho a seguir. Com a Secret 2.0, vamos nos aventurar na direção de misturar diferentes técnicas na pilha para dar aos desenvolvedores a escolha que melhor se adapta ao seu caso de uso.

Na Parte 3 desta série “Beyond ZK”, vamos nos aprofundar em uma pilha de privacidade modular para blockchain e o que ela permite para o problema de computação segura. Se você estiver interessado em dar uma olhada nos projetos modulares de privacidade, sinta-se à vontade para ler nossa postagem no blog sobre a Secret 2.0, explicando a próxima evolução da Secret Network!

O que está por vir?

Pensamos profundamente sobre essas questões nos últimos anos, e a Secret Network tem orgulho de continuar liderando o esforço em direção à computação segura no espaço blockchain. Se essas ideias lhe interessam — e se você está convencido de sua importância — junte-se a nós na criação de soluções e tecnologias que podem nos ajudar a proteger a Web descentralizada e dimensionar a Web3!

Se você for um desenvolvedor de aplicativos, confira nossos recursos aqui. (Secret usa Rust!)

Se você é alguém apaixonado por garantir que os usuários do Web3 tenham as proteções de privacidade de dados de que precisam e merecem, considere se tornar um agente secreto ! É nossa missão garantir que a web descentralizada que estamos construindo seja uma que realmente capacite — e que seja acessível a todos. Da conscientização e educação ao crescimento internacional e relações universitárias, há muitas maneiras de ajudar a contribuir para a expansão do ecossistema Secret e a disponibilidade global de tecnologias de privacidade na Web3.

Confira o programa Secret Agents e junte-se a uma das melhores e mais comprometidas comunidades em todo o espaço blockchain!

Como se tornar um agente secreto

Avante e para cima em direção à privacidade!

Guy Zyskind é o fundador da Secret Network, CEO da SCRT Labs, ex-pesquisador do MIT e autor de alguns dos documentos de privacidade de blockchain mais citados (incluindo “ Descentralizando a Privacidade ”, escrito em 2015).

Dúvidas e caso queira se envolver no projeto da Secret Network, junte-se a nossas redes:

Telegram Secret em português: https://t.me/secret_portuguese

Canal Youtube Secret Network em português: https://www.youtube.com/c/SecretNetworkHubPTBR

Twitter Secret português: https://twitter.com/scrt_portuguese

Instagram: https://www.instagram.com/secretportuguese/

Discord: https://discord.gg/Ug5yx3MN